HOME         PROBLEMS SOLVED         PHYSICAL SUPPORT         PREDICTIONS         PUBLICATIONS         PRE-PRINTS

Every century or so, an advance is made that changes how we understand the foundations of physics. Some physical principles evolve from one mode of thought to the next. And sometimes the principles on which our understanding of nature are built, change. We call such changes a shift in paradigm.

By example, Ptolemy envisioned that the Earth was at the center of the universe. He also advanced the idea that planets moved in circles around the Earth. To account for their motions required an elaborate collection of geometric principles.

This paradigm continued until the time of Copernicus, who advanced the idea that the Earth and planets orbited the sun. He also argued for circles, so while the change was significant, it was only part of a much larger solution.

Kepler offered yet another change. His argument was that planets followed paths other than circles, namely ellipses. The need for offset circles and epicycles were no longer needed.

Newton, the father of physics, set forth the principles of calculus. He resolved many of the most fundamental laws of nature, much as we use them today. He shifted the paradigm, arguing that the laws of nature applied as much to the heavens as they did on Earth. That is, the same motions that directed the paths of planets also directed apples falling from trees.

Einstein introduced yet another shift in paradigm. He argued that the notion of measure was not absolute. He also argued that the speed of light was constant for all observers. And he proposed the equivalence principle, that the behavior of inertial and gravitational frames were equal and indistinguishable.

Measurement Quantization (MQ) offers a new paradigm for consideration. With MQ we recognize that all the existing laws of physics are resolved with respect to the discrete Internal Frame of the universe. As the System Frame of the universe has no external reference, MQ finds that the System Frame must be non-discrete. And when considering the difference between these descriptions, we resolve expressions and values for the physical constants and the laws of nature. Importantly, these values match our best measurements digit-for-digit to the same precision as our best available measurements.

So what is MQ? In simplest form, MQ is a physically significant nomenclature. We take existing classical expressions and write them in terms of counts n_L, n_M, and n_T of fundamental measures - l_f, m_f, and t_f. When written as such, expressions reduce to either counts, measures or the fundamental expression. A notable example includes Heisenberg's uncertainty principle 2n_Lrn_Mn_L=n_T. This expression - when considering the boundary condition - has been reduced to find that all measure terms cancel, leaving only the counts. Consider then, when discussing the Planck Scale, how could the uncertainty principle describe measure, when there are no measure terms?

In the same way, using MQ helps us recognize that space cannot be curved in a physically meaningful way. References, by definition, have no smaller features. In that a curved space is made up of smaller considerations of length, and the fundamental length reference (i.e., the Planck length relative to the observers frame) is the smallest length having physical significance, how could curved space be physically significant? MQ demonstrates that the appearance of curvature is actually a function of lost fractional counts of length with each increment in elapsed time t_f. That loss, is the phenomenon of gravity.

We might ask, can we prove MQ is physically significant? Yes. This has been accomplished in multiple ways. The easiest regards the most basic prediction of MQ, that measure relative to the internal frame is quantized. If measure with respect to the Internal Frame is discrete, then would not the loss of the non-discrete portion of a more precise calculation also describe length contraction? And could this length contraction be resolved from existing measurement data?

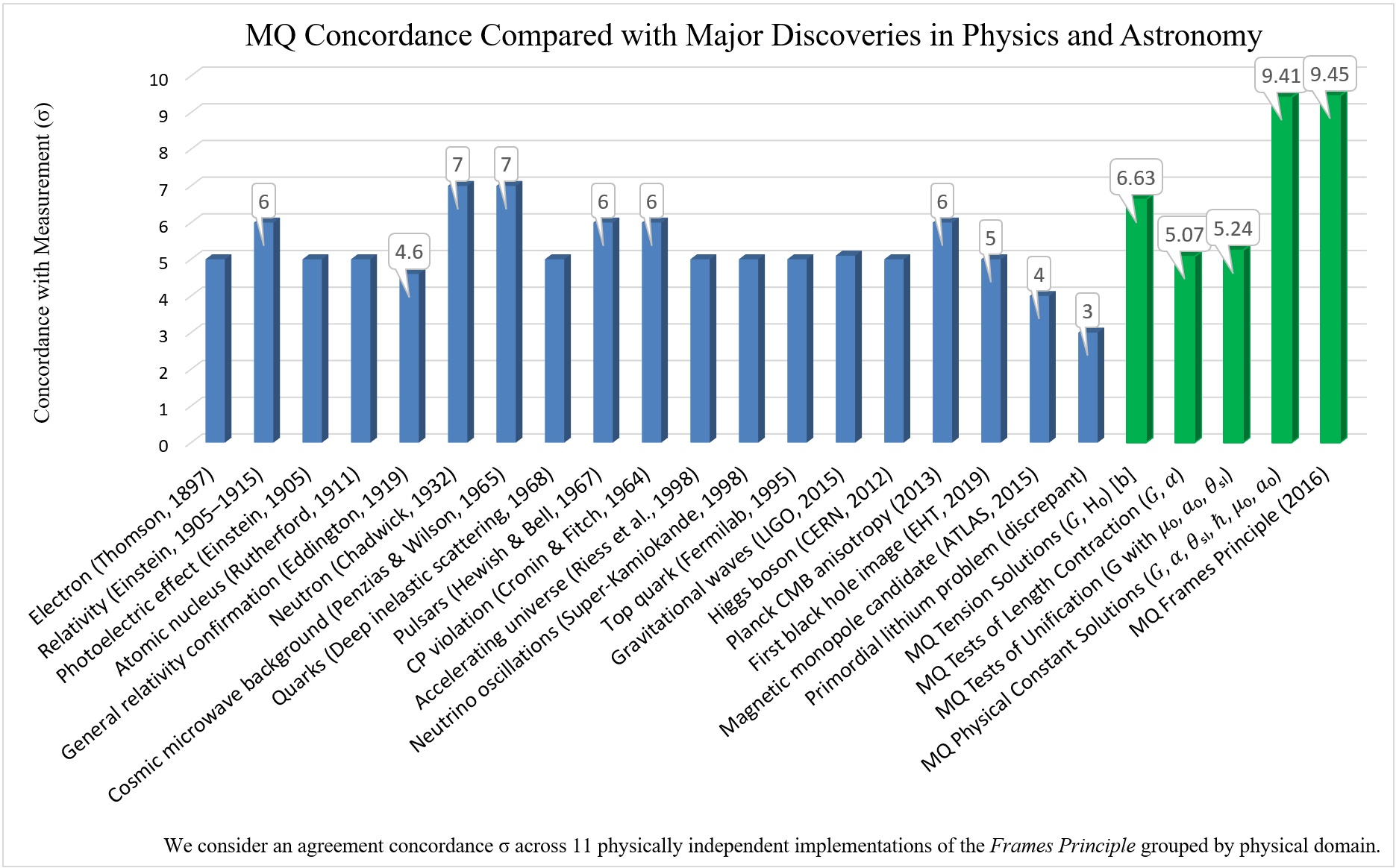
We call this effect the Informativity differential. It is not related to relativity; it is an entirely new form of length contraction. And it can be resolved with respect to each publication of the CODATA physical constants. We've carried out the calculations in this paper, thus resolving the experimental conditions of each proposed value for G and ħ for the 2010, 2014, and 2018 CODATA publications. The results match the calculations digit-for-digit.