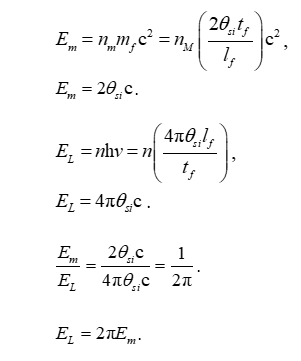—————————— read pre-print on research gate (new window) ——————————

• h is Planck’s constant.
• ħ is the reduced Planck constant, 1.054571817 10^-34 m² kg s^-1. When accounting for the Informativity differential at the upper count bound, this term is not italicized (i.e., ħ=1.0545349844(45) ^-34 m² kg s^-1).
• π is a numerical value describing the arc-distance of a circle of radius one.

• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• n_M is the count of m_f representing the mass corresponding to a gravitational field.
• Q_L is the fractional portion of a count of l_f when engaging in a more precise calculation.
• n_Lr describes the count of l_f representative of the position of an observable with respect to the frame of a center of mass.
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.
• v is velocity measured between an observer and a target.
• m is an observed mass.
• E_l is the energy of one quantum of electromagnetic radiation.
• E_m is the energy of half a fundamental unit of mass *m_m.

Using the Measurement Quantization (MQ) approach to describing Einstein and Planck’s expressions for energy reveals a more fundamental correlation than presently resolved using Planck's expressions. The difference in a fundamental unit of energy with respect to each is 2π. This has always been interpreted, for instance, as the difference between the momentum and angular momentum of the respective phenomenon. MQ allows us to extend our understanding, distinguishing between the component measures l_f, m_f, and t_f and the scalar and counts n_L, n_M and n_T.

Writing each expression in terms of the MQ nomenclature - such that we account for the discrete features of measure with respect to the three frames of reference - the System and Internal Frames of the Universe and the Reference Frame of the observer - and such that Planck's expression is resolved as E=nhv, we find that n must be 1/2π. This is to say, that the count n is currently ascribed an angular description of one full circle. We ask, is such a description a physical or geometric property of the phenomenon?

With MQ, we have the opportunity to step back and look at each of the two descriptions using a physically shared nomenclature l_f, m_f, and t_f, resolved as an emergent property of the expanding frame of the universe. Reducing each of the energy expressions to the fundamental measures we can now ask questions which before did not lead to definitive physical conclusions.

For example, note that the energy of a fundamental unit of mass is E_m=2θ_sic. Such that 2θ_si is the radial rate of expansion for the universe H_U, and c is the rate of expansion relative to a point on its leading edge, we find that the energy of a fundamental unit of mass is a product of the expansion parameter over the perimeter velocity times the age of the Universe A_U. The expression describes what the mass reference looks like using terms that describe the expansion of our universe as observed.

Additional insights are offered in the noted preprint. The paper resolves, specifically, the difference as a quality associated with the Internal and System Frames. Depending on which frame is considered, a phenomenon inherits different local properties. The difference between these frames also derrives expressions and values for the physical constants and the laws of nature.