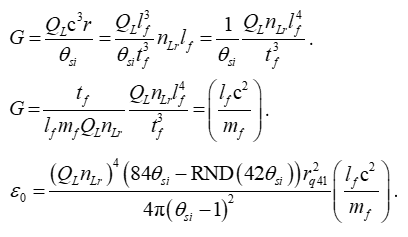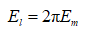—————————— read pre-print on research gate (new window) ——————————

• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.

• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• G is the gravitational constant, 6.6740779428(56) 10^-11m³kg^-1s^-2 such that its value considers the effects of length contraction associated with discrete measure at the upper count limit. Italicized G identifies a measure not at the limit (e.g., G=6.6738448362(53) 10^-11m³kg^-1s^-2 at the blackbody demarcation).
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.
• Q_L is the fractional portion of a count of l_f when engaging in a more precise calculation.
• n_Lr describes the count of l_f representative of the position of an observable with respect to the frame of a center of mass.
• Δ_fr is the metric differential; describes the numerical difference in distance between the discrete and non-discrete frames of reference
• γ is gamma. As demonstrated with an MQ description of the physical constants, gamma describes the four geometries that separate a description of gravitation from that of electricity
• ɛ₀ is the electric constant
• E_l is the energy of one quanta of electromagnetic radiation
• E_m is the energy of one fundamental unit of mass m_f

Support is offered by way of physical correlation of MQ descriptions of the physical constants with their classical counterparts. Notably, the differences described below represent the effects of length contraction associated with discrete measure relative to the Internal Frame of the universe. We call this effect, the Informativity differential. Once accounted for, there is no difference between calculation and measurement with digit-for-digit correspondence to the same precision as our best measurements.

We bring to the reader's attention that while the MQ approach recognizes the importance of measure with respect to the demarcation associated with a phenomenon, classical measurement does not. Therein, to assure physical consistency, MQ calculations must resolve values such that all measurements are made either macroscopically or at the electromagnetic demarcation.

One might expect given the considerable effort over many decades to unify gravitation with electromagnetism, that the solution would be immensely complex. But this presumes that their relation is easily separated from the observer's frame of reference. This is not the case.

For one, modern theory does not explicitly recognize the System or Internal Frames of the universe. Importantly, the effects described by the Informativity differential are not accounted for. For this reason, using measures of the physical constants that are each resolved using a common frame of reference is important.

The Measurement Quantization (MQ) approach to classical expression addresses these issues. MQ is advanced with a new approach to the description of gravitational curvature that is discrete. The properties of measure are resolved by considering the application of an MQ nomenclature to Heisenberg's uncertainty principle - specifically an analysis of the Planck scale bound - escape velocity and the speed of light. With this, we can demonstrate that measure with respect to the Internal Frame is discrete and countable, a function of fundamental references and counts of those references for the notions of length, mass and time. In that the universe has no external reference, we also recognize that the System Frame of the universe is non-discrete.

Therein, where the electric and magnetic constants are inversely proportional (i.e. ɛ₀=1/u₀c²) we consider only the relation between G and ɛ₀. For each, we move the dimensional terms to the right.

The dimensional terms for the electric constant include terms that also describe gravitation. We make the substitution.

Of importance is the frame transform that separates the two phenomena. Notably, we find the expression a composite of four geometries and a mathematical constant, the latter which describes the energy difference between a fundamental unit of energy describing a baryon and photon. We will explain each.

• Two measurement-distortion phenomena: the metric and Informativity differentials
The Informativity differential is described by Q_Ln_Lr at 42_θ_si_ and the metric differential is described by Δ_fr. Each describe a relative skew in measure. The Informativity differential addresses the skew in l_f with respect to the discrete Measurement Frame of the observer. The metric differential addresses the scalar between frames, as a function of θ _si.

• First frame correlation: the metric differential associated the fine structure constant
With the inverse fundamental fine structure constant 42θ _si, we apply the metric differential to resolve the Planck equivalent expression. The expression is a count of θ _si corresponding to the blackbody demarcation.

• Second frame correlation: the metric differential associated with elementary charge
This expression describes the metric differential associated with elementary charge. The expression correlates the value of e between the discrete and non-discrete frames. Notably, we use the discrete offset to resolve the measurement distortion created by the frame differential. The approach is physically correct, but not - in the author's opinion - complete. There is some possibility that e cannot be resolved without the introduction of a new understanding of the construct of the universe.

• One particle/wave correlation: as a function of energy
The last term is 2π. This term describes the energy difference between a fundamental unit of mass m_f and a quantum of electromagnetic action.

Such that γ represents those geometries associated with the System and Internal Frame difference and, specifically, are not intrinsic properties of either phenomenon, we isolate those terms.

Thus, the final expression describing the physical relation between G to ɛ₀ is

The relation follows the same form as that for fundamental energy, E_l=2πE_m.

We call attention to the difference between these phenomena consists of only two features, the frame difference and the energy difference, both which demonstrate a geometry.