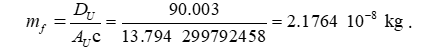—————————— read pre-print on research gate (new window) ——————————

A_U is the age of the universe.

• H is the value of H0 m s-1Mpc-1 when resolved with respect to universal expansion (i.e., the Target Frame).
• H_U is the rate of universal expansion with respect to the diameter of the universe (per D_U). This differs from stellar expansion (i.e., Hubble’s description).
• *H_f is the Hubble frequency.
• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.
• n_Lu is a count of l_f equal to the diameter of the universe.

There are several tens of notable experiments that measure the rate of expansion of our universe. Rather than provide an on-going citation of those experiments we refer the reader to this regularly updated list kept on Wikipedia:

https://en.wikipedia.org/wiki/Hubble%27s_law

Notably, the most recent experiments still continue to find results that support the calculations arrived at using the Measurement Quantization (MQ) approach. Example 2019 results are summarized here:

1. 2019-08-15 73.5±1.4 Riess, A. G.; Pesce, D. W.; Reid, M. J. (15 August 2019). "An Improved Distance to NGC 4258 and its Implications for the Hubble Constant". Retrieved 16 August 2019.
2. 2019-07-16 69.8±1.9 Sokol, Joshua (19 July 2019). "Debate intensifies over speed of expanding universe". Science. doi:10.1126/science.aay8123. Retrieved 20 July 2019.
3. 2019-07-10 73.3+1.7−1.8 Sidney van den Bergh (2019). "H0LiCOW XIII. A 2.4% measurement of H0 from lensed quasars: 5.3σ tension between early and late-Universe probes", arXiv:1907.04869
4. 2019-07-08 70.3+5.3−5.0 Hotokezaka, K.; et al. (8 July 2019). "A Hubble constant measurement from superluminal motion of the jet in GW170817". Nature Astronomy: 385. arXiv:1806.10596. Bibcode:2019NatAs.tmp..385H. doi:10.1038/s41550-019-0820-1. Retrieved 8 July 2019.
5. 2019-03-28 68.0+4.2−4.1 Domínguez, Alberto; et al. (28 March 2019), A new measurement of the Hubble constant and matter content of the Universe using extragalactic background light γ-ray attenuation, arXiv:1903.12097v1
6. 2019-03-18 74.03±1.42 Riess, Adam G.; Casertano, Stefano; Yuan, Wenlong; Macri, Lucas M.; Scolnic, Dan (18 March 2019), Large Magellanic Cloud Cepheid Standards Provide a 1% Foundation for the Determination of the Hubble Constant and Stronger Evidence for Physics Beyond LambdaCDM, arXiv:1903.07603
7. 2019-02-08 67.78+0.91 −0.87 Ryan, Joseph; Chen, Yun; Ratra, Bharat (8 February 2019), "Baryon acoustic oscillation, Hubble parameter, and angular size measurement constraints on the Hubble constant, dark energy dynamics, and spatial curvature", Monthly Notices of the Royal Astronomical Society: 1893, arXiv:1902.03196

The fundamental expression l_fm_f=2θ_sit_f can be extended such that a count of the fundamental measure of length l_f divided by a count of the fundamental measure of time t_f representative of the radius R_U and age A_U of the universe describes its expansion. The correlation, at first sight, appears overly simplistic. This is concerning as it is as though we have assumed that the rate of expansion is an equality with the fundamental measures, and as such describes a flat universe. Physical support for this claim is provided by paradox and physical support by comparing CMB measurements with calculated values.

MQ descriptions of universal expansion are an extension of those principles argued by Einstein, but offer greater precision across the entire measurement domain. With an MQ understanding of nature there are three physically significant frames: the reference frame of the observer, the discrete Internal Frame of the universe and the non-discrete System Frame of the universe. Considering the difference between these frames allows us to resolve expressions and values for the physical constants.

We begin, as such, describing expansion as a property of the Internal Frame. Length, mass and time are each emergent properties of the system. With this in mind, we reexamine these phenomena as properties of the fundamental expression.

Given elapsed time and considering the fundamental expression, such an analysis demonstrates specific rates for increasing length and increasing mass independently. Increasing length is as recognized a quality associated with the dark energy phenomenon. Mass accretion, though, is a prediction of MQ. The rate of mass accretion M_acr is found to be constant during both the quantum and expansionary epochs. We can use M_acr to calculate the accumulated equivalent mass corresponding to the trigger event which then identifies that point that marks the transition from a quantum epoch to the expansionary epoch. The calculation of accumulated mass, corresponding to what we measure today as the CMB, match our best observational data, five significant digits. We can also use the expression for M_acr to calculate the mass of the universe today. This calculation matchs to five significant digits, based on CMB measurements of the age of the universe. Finally, we can use M_acr to validate a description of galactic rotation, again a match, having a 1.6 km/s standard deviation with respect to star velocities in the Milky way relative to the first 85,000 light-years. But, let us start with physical support that can be confirmed in the laboratory. For instance, expansion can be correlated with a calculated measure of a fundamental unit of mass m_f.

We should note, the rate of expansion 2θ_si is defined with respect to the system, the universe. Traditionally Hubble's constant is defined per megaparsec. We will convert the measurement for you shortly. But, for now we continue with citations of physical correspondence, such as this expression containing the gravitational constant

In addition to the above cosmological expressions for m_f, universal expansion and the relative values for the fundamental measures, l_f, m_f and t_f are correlated. That is to say, had the rate of expansion as defined with respect to the system - the universe - been different, then the fundamental measures would have differing values. If this rate of expansion varied over time, then the values of the fundamental measures would also vary relatively. Such a proposition would be difficult to maintain as it would also imply that such variation had occurred in the past and where the values of the fundamental measures are implicit to the radial distance of electrons about atoms, such change would be reflected in the spectral lines of stars that form in the early universe. Moreover, there is some question whether such atoms would be stable. MQ presents a framework in which we can offer physical support that what is observed corresponds to a flat universe with a constant rate of expansion and that such a description follows the expressions resolved using MQ.

With respect to the 2010 CODATA we demonstrate that this measure makes use of an electromagnetic field, specifically the MSL-03 electrostatic compensation approach. The 2014 CODATA publication relies on a macroscopic approach, specifically the HUST-18 time-of-swing approach. The Informativity differential, that is the degree of length contraction is very different as a function of relative distance, increasing with shorter distances. For this reason, we must be sure to use measures of terms that all derive from a shared frame distance. The least problematic, is to use a calculated macroscopic measure of the reduced Planck constant along with the 2014 measure of G. Notably, the 2018 CODATA publication presents a measure of G inconsistent with the allowable physical domain. In the paper entitled, Measurement Quantization, we demonstrate that this result is resolved as a misapplication of Planck's expressions in the calculation. Depending on the experiment, the result also falls within the measurement uncertainty of several approaches.

Also at work in the expansion of the universe are the effects described by relativity. Those effects are usually ignored in modern theory in that a means to resolve the time dilation between the quantum and expansionary epoch is not possible without a physical model that identifies the trigger between them. MQ provides a complete picture and a trigger.

Yet another approach, the value of the expansion parameter θ_si can be measured as the angle of polarization for the signal and idler of X-rays in Bell states at their degenerate frequency. Bear in mind, we only show that the magnitude is equal and do not imply that angle and momentum are in any other way comparable. The calculations and measurement data can be found in the section labeled 'Quantum Entangled X-rays'. The expansion parameter can also be measured with respect to gravitational curvature. θ_si is also present when defining Planck's constant and in expressions that describe galactic rotation. Importantly, resolving θ_si does not assume a flat universe - a universe without curvature - when recognizing the physical significance of frames of reference. This quality of the universe is resolved as a property of measure and presented in the paper entitled, Measurement Quantization Describes the History of the Universe....

The expressions above describe what in MQ is call universal expansion, the rate at which space expands. In contrast, we identify the rate at which galaxies move away from one another as stellar expansion. In practice, the two measures are nearly one and the same, differing only by the smallest of value due to the force of gravitation since the earliest epoch. Given the rate of universal mass accretion and the upper count bound to the observation of mass per increment of elapsed time (the fundamental unit of time), the effects of gravitation at the galactic scale over the history of the universe are - in all liklihood - physically insignificant.

To assure no confusion in symbols, we identify universal expansion when written in units Mpc^-1 with the symbol H. We identify universal frequency, that being the inverse of the universal expansion parameter with H_f. And finally, where universal expansion is defined per the diameter of the universe (as opposed to per megaparsec), we use the symbol H_U. It is as such, that the calculation of universal expansion is

The expansion parameter 2θ_si describes the rate of expansion when defined with respect to the diameter of the universe. From this we resolve that the rate is constant. We also find that there is no faster-than-light inflationary period. To be clear, there is no predicted inflationary period. The early universe is characterized by a period of quantum expansion that lasts for 363,312 years. Specifically notable, the calculations are a consequence of the discrete internal frame. They unfold without the need for a premise or conjecture.