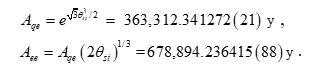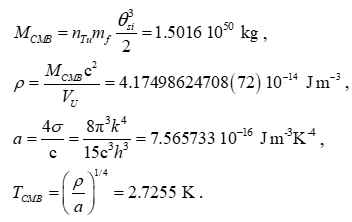—————————— read pre-print on research gate (new window) ——————————

• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• n_Tu is a count of t_f equal to the age of the universe.
• σ is the radiation constant.
• k_B is the Stefan-Boltzmann constant.
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.
• h is Planck’s constant.
• ħ is the reduced Planck constant, 1.054571817 10^-34 m² kg s^-1. When accounting for the Informativity differential at the upper count bound, this term is not italicized (i.e., ħ=1.0545349844(45) ^-34 m² kg s^-1).
• V_U is the volume of the universe.

• R_U is the radius of the universe.
• A_U is the age of the universe.
• A_ee is the dilated age of the universe as measured from the current expansionary epoch. Its value is a function of expansion with respect to the total elapsed time representing the quantum epoch.
• A_qe is the non-dilated age of the universe corresponding to the quantum epoch.
• M_tot is the total mass of the universe, including all forms of energy.
• ρ is the energy density accumulated at a given age of the universe.
• a is the total energy radiated as described with respect to blackbody radiation (i.e., the Stefan-Boltzmann law).
• σ is the radiation constant.
• T_CMB is the temperature of the Cosmic Microwave Background.

Using a Measurement Quantization (MQ) nomenclature with existing classical expressions we resolve a description of early universe events. Most notable, there is no prediction of an inflationary period. Rather, we find a 363,312 year quantum period during which the universe expands at a quantum pace. The expressions of MQ also describe a universe with a fixed rate of increasing mass.

When combining both descriptions we can calculate the mass accretion during the quantum epoch, and using separate measurements for the age of the universe we can resolve the present-day density and temperature of this accretion. As expected, the accretion is today observed as a Cosmic Microwave Background (CMB) and those calculations match digit-for-digit a Fixsen study of CMB temperatures, which aggregates several studies made over a ten year period prior to his 2009 publication.

Therein, we can walk through these calculations beginning with a summary of what MQ is. It is a physically significant nomenclature such that existing classical expressions are described using counts n_L, n_M, and n_T of fundamental reference measures l_f, m_f and t_f. These measures have previously been known as the Planck units, but could not be shown to be physically significant and in part, could not be solved for.

Using a discrete description of gravitational curvature along with discrete descriptions of Heisenberg's uncertainty principle, escape velocity and the speed of light, we can demonstrate that measure with respect to the Internal Frame of the universe must be discrete. And such that the universe has no external reference, we can also show that measure with respect to the System Frame of the universe is non-discrete. And when considering the difference between these frames we can resolve expressions and values for the physical constants and the laws of nature.

Therein, we present the argument, that the universe initially expands at a quantum pace as points in the Internal Frame are unable to discretly access points external to the universe. This can be resolved mathematically such that the first discrete count is

units of l_f. As such, the rate of expansion was slowed. We can calculate that expansion such that,

The epoch lasts for 363,312 years. When comparing elapsed time across both epochs we find time dilation.

Thus, when calculating the total mass accretion during this epoch in terms - with respect to - the present epoch, we must multiply the rate of mass accretion by the dilated age, 678,894 years. It's important to note that the calculation is not solved for, but a direct consequence of the independently calculated expressions, such that the dilation is resolved by multiplying by the cube root of two times the radial rate of expansion.

And with this we resolve the total accreted mass and its present-day density and temperature.

There are two points of interest in this calculation.

One, when the universe reaches a radius of square root of five l_f, why doesn't expansion cease and return to a quantum crawl? Notably, once the universe has begun expansion, there are new points within the quantum bubble that are able to reference points externally. Not only will expansion continue, we propose that the uneven nature of these reference points led to the shape of the universe we observe as internal occupants.

A second point of interest regards mass accretion during the quantum epoch. How do we know that some mass did not carry over in baryonic form to the expansionary epoch? To this we respond that MQ offers guidence. Specifically, there exists a maximum baryonic density such that there can never be more than one unit of fundamental mass for each two units of fundamental length. Therein, we conclude that effectively all of the accreted mass must today be represented by the CMB.

Additional questions regard the flatness problem, the horizon problem and the monopole problem. We won't address these in detail as they are each explored in the linked pre-print awaiting publication. But we will note that a 363,312 year quantum epoch establishes the conditions necessary to resolve all three issues. During this period, we find a universe that is homogenous and isotropic. The flatness problem is resolved separately, a property of our universe that reflects an expansion of the fundamental expression.