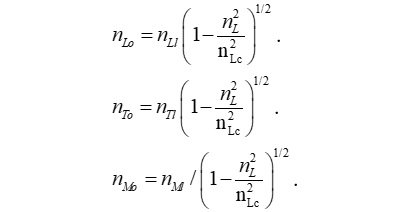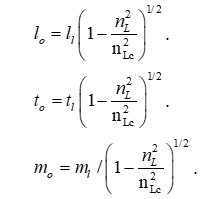—————————— read pre-print on research gate (new window) ——————————

There are no inputs needed to resolve these expressions.

• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• n_Lc describes the count of l_f* representative of a change in position of light measured with respect to the observer’s frame of reference.
• n_Lo is the count of l_f observed with respect to the observer’s frame of reference.
• n_Ll is the count of l_f measured with respect to the observer’s frame of reference.
• n_L, n_M and n_T are physically significant discrete counts of l_f, m_f and t_f respectively.
• Q_L is the fractional portion of a count of l_f when engaging in a more precise calculation.
• l_l is a measure of length with respect to the observer’s measurement frame.
• l_o is the observed length subject to the effects of motion and/or gravitation.
• m_l is a measure of mass with respect to the observer’s frame of reference.
• m_o is the observed mass subject to the effects of motion and/or gravitation.
• t_l is a measure of time in the local frame of reference.
• t_o is the observed time subject the effects of motion and/or gravitation.
• v is velocity measured between an observer and a target.
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.

Einstein’s approach to describing the contraction and dilation of measure differs from that when using Measurement Quantization (MQ). So, what has changed?

Frames of reference. Einstein envisioned classical behavior as a non-discrete function of two frames, that of the observer and that being observed. This is sometimes described with respect to a train moving down tracks, such that we consider what is experienced by an observer on the train relative to an observer standing near the tracks. This model of understanding has served well with incredible precision.

One would think there was nothing more that could be added to improve such a model. But there is where we consider the MQ framework. MQ utilizes and expanded classical nomenclature. That is, we describe phenomena as a function of fundamental measures l_f, m_f, and t_f and counts of those measures, n_L, n_M, and n_T. We also recognize three frames of reference, discrete Reference Frame of the observer, the discrete Internal Frame of the universe and the non-discrete System Frame of the universe. And where the notions of length, mass and time are shown to be a discrete function of fundamental references, we can demonstrate that measure is both discrete and countable with respect to the Internal Frame.

It follows by the same physical support that the frame of the universe must be non-discrete, in that the universe can have no external reference.

One approach to verifying these claims regards a new form of length contraction not related to relativity. We call this effect the Informativity differential. It is resolved as the non-discrete portion of the hypotenouse of a right-angle triangle as resolved with a more precise calculation of sides a and b. This effect has been published, physically demonstrated using existing data from CODATA publications in 2010, 2014, and 2018.

With this foundation, we approach relativity in a very different fashion. We begin with the Pathagorean theorem, such that the first term describes the maximum range of possible values, the second term describes the minimum range of possible values and the final term describes unity. All terms are correlated to their count bound.

With respect to the observed frame, a (i.e. the count change in distance n_Ll) can take any value from 0 to n_max. With respect to the local frame, b (i.e. n_Lo) can take any value from 0 to n_min. The result is an expression that describes all possible events with respect to length and motion.

We can for convenience also introduce the fundamental measures back into the expressions, thus removing some of the count terms. The expressions match Einstein’s with one important difference; these expressions are discrete. Recognition of count bounds is essential to avoiding singularities as so commonly occur in classical theory.

We bring a final observation to the attention of the reader. Singularities cannot occur with respect to an MQ description of nature. Such that all counts are physically significant where integer, equal or greater than one, we are not afforded with the opportunity for singularities.