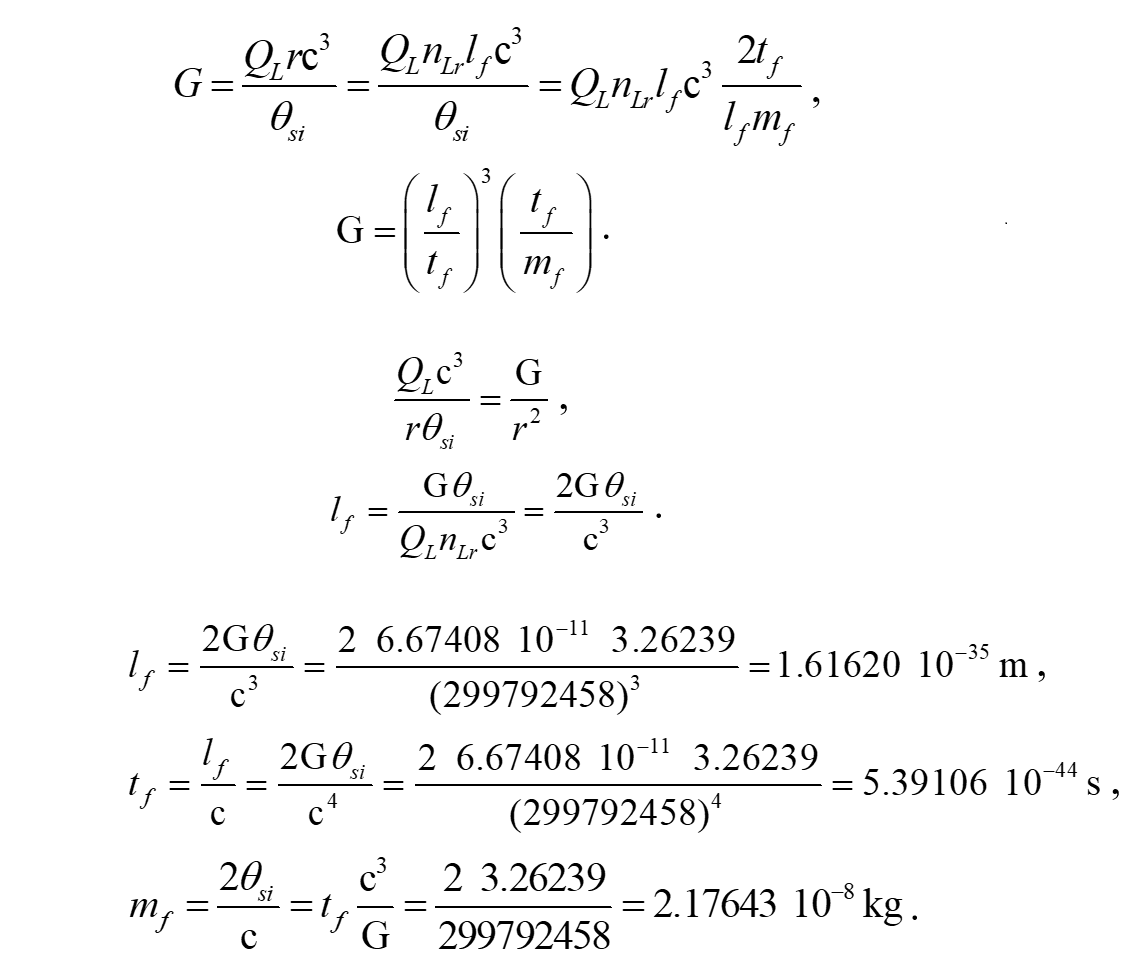what defines the Fundamental Measures?
Fundamental Measure
Length: lf
Mass: mf
Time: tf
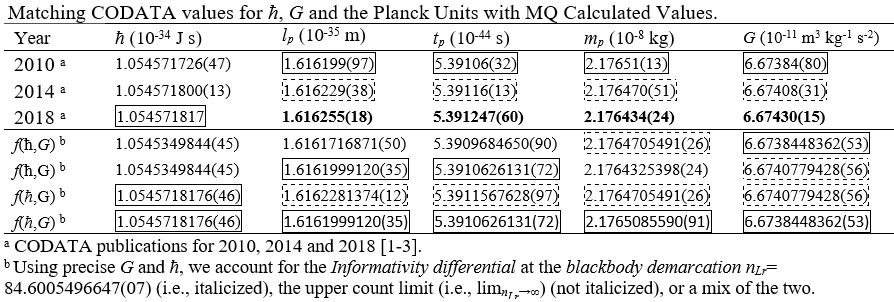
2014 CODATA Measure
1.616199 10-35 m
2.17647 10-8 kg
5.39106 10-44 s
MQ Calculation
1.616200 10-35 m
2.17647 10-8 kg
5.39106 10-44 s
Inputs
- θsi can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θsi=3.26239 rad ± 2 μrad; as a momentum θsi=3.26239030392(48) kg m s-1 and with respect to the Target Frame, θsi has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al..
- c is the speed of light which may also be written as c=nLlf/nTtf=299,792,458 m/s such that nL=nT=1 is physically significant.
- G is the gravitational constant, 6.6740779428(56) 10-11m3kg-1s-2 such that its value considers the effects of length contraction associated with discrete measure at the upper count limit. Italicized G identifies a measure not at the limit (e.g., G=6.6738448362(53) 10-11m3kg-1s-2 at the blackbody demarcation).
Terms
- lf, mf and tf are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
- QL is the fractional portion of a count of lf when engaging in a more precise calculation.
- nLr describes the count of lf representative of the position of an observable with respect to the frame of a center of mass.
Calculations
Experimental Support
[1] P. Mohr, B. Taylor, and D. Newell, CODATA Recommended Values of the Fundamental Physical Constants: 2010, p. 73 (2012), arXiv:1203.5425v1, doi:10.48550/arXiv.1203.5425.
[2] P. Mohr, B. Taylor, D. Newell, CODATA Recommended Values of the Fundamental Physical Constants: 2014, p. 3, (2015), arXiv: 1507.07956v1, doi:10.1063/1.4954402.
[3] NIST: CODATA Recommended Values of the Fundamental Physical Constants: 2018, (May 2019), https://physics.nist.gov/cuu/pdf/wall_2018.pdf, doi:10.1103/RevModPhys.93.025010.
Discussion
The fundamental measures are physically significant and their significance may be demonstrated with our existing understanding of Heisenberg’s uncertainty principle. Specifically, in the case of describing the position and momentum of a particle at the Planck Scale bound σXσP≥ħ/2 we can substitute the terms for standard deviation with their corresponding classical descriptions, written using a Measurement Quantization (MQ) nomenclature. That is to say, we can describe the position of the particle as a count nLr of fundamental units of length lf. And we can describe the particle's momentum as the product of a count nM of a fundamental unit of mass mf at a change in distance count nL of a fundamental unit of length lf from the observer. With this nomenclature we then reduce the expression.
Importantly, the reduction reveals a discrete description of gravitational curvature relative to the Internal Frame of the universe. This feature of the derivation is missing from modern theory, thus providing only for its solution using Planck's unit expressions. But the Planck units, having no specific grounding as to their physical significance, are no different than any other scaling of the measurement system (i.e., SI units, Stoney units, Emperial units). MQ offers a solution to gravitational curvature not previously considered and with this we provide a physically correlated reduction of the uncertainty principle.
Equally important to the resolution of the fundamental measures, we use the the expressions for Heisenberg's uncertainty principle, escape velocity and the speed of light, to resolve the three properties of measure. Specifically, that measure is
- discrete,
- countable,
- and a function of the Reference, Internal and System Frames.
Therein, we resolve values for each dimensional count term. We combine this with the MQ description for gravitational curvature to resolve values for each of the fundamental measures not as a function of G, c and ħ, but instead as a function of lf, tf and the fundamental constantθsi. Notably, the MQ form of the gravitational constantG=(lf/tf)3(tf/mf) and the speed of light c=lf/tf are each a function of the fundamental measures, but their values are neither assumed nor preprequisite to their evaluation.
Therein, the fundamental measures differ from Planck's formulations. As such Planck's units are distinguished with a subscript p. The physical difference between each set is described by the Informativity differential.
The Informativity differential describes a length contraction effect similar but not related to that described by relativity. The magnitude of this effect is a function of distance - increasing with decreasing distance - and is physically significant in the measure of G (which is typically measured macroscopically) and in the measure of ħ (which is measured quantumly as a function of blackbody radiation). An analysis and explanation of how the Informativity differential affects G and ħ may be found in the article that covers the Newton and Planck constants.
Quantum Inflation, Transition to Expansion, CMB Power Spectrum