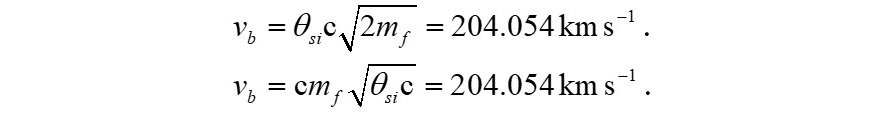—————————— read pre-print on research gate (new window) ——————————

• θ_si, is 3.26239 radians or kg m/s (momentum) or no units at all a function of the chosen frame of reference. This is a new constant to modern theory and exists in nearly every equation of the model. It may be measured macroscopically given specific Bell states necessary for quantum entanglement of X-rays such as those carried out by Shwartz and Harris.
• l_f, m_f and t_f are effectively Planck’s Units for length, mass and time, but not precisely the same. In MQ we recognize them as the fundamental units.
• c is the speed of light which may also be written as c=l_f/t_f=299,792,458 m/s.
• *v_m*is the modelled velocity. Both v_e and v_m describe a constraining function. When one is incorrect, the two curves diverge.

• v_e is the escape velocity of a mass from a gravitational field.
• v_b is the bound velocity which represents that velocity when mass events exceeds the upper count bound due to measurement quantization
• G is Newton’s gravitational constant, 6.67408 10^-11 m³ kg^-1 s^-2.
• R is the distance between a center of gravity and the orbital distance of a star being considered.
• M_e is the effective mass of a system that corresponds to that mass experienced by an inertial frame.
• M_b is the bound mass, which represents the unadjusted upper bound to mass events that can be distinguished.

Stacey McGaugh, "Milky Way Mass Models and MOND (2008)" ApJ, 683, 137-148

Stacey McGaugh, A Precise Milky Way Rotation Curve Model for an Accurate Galactocentric Distance (August 2018) Res. Notes AAS, 2, 156, doi:10.3847/2515-5172/aadd4b.

The phenomenon known as dark matter includes two unexplained observations. One, the velocity of stars orbiting a galactic core is many times faster than that described by Newton's expression for an orbital mass. Two, as we consider stars further from the galactic core we expect velocities to decrease. This is not observed.

Using the Measurement Quantization (MQ) approach to classical expression we offer new expressions which demonstrate a standard deviation of 1.394 km/s with respect to the first 84,000 lightyears of Milky Way star velocity data. Its physical significance is established by demonstrating that the notions of measure - length, mass, and time - are a composite of fundamental reference measures relatively defined with respect to the Internal and Systems Frames of the universe. Such that the universe has no external reference, we also recognize that measure with respect to the System Frame of the universe is non-discrete. Considering the difference between the discrete and non-discrete frames we can derive expressions and values for the physical constants.

Star velocities are resolved by incorporating two principles; one, the expansion of the universe and two, the upper count bound to fundamental mass m_f. We call this the upper bound the mass frequency bound (represented by the purple curve in figures 1 and 2).

Using a nomenclature of counts of physically significant reference measures, we can then approach a description of galactic orbital dynamics. First, we resolve the bound velocity as a function of the mass frequency bound. The expression takes into account expansion but does not account for the mass profile of a galaxy.

Both expressions are equivalent, but use different terms. With reference to the first, the radial expansion of the universe is described by the value θ_si. The upper bound to countable mass measures is described by c times the square root of 2m_f. Collectively, the expression describes the effective velocity as a function of the upper count bound of measurable mass (i.e., the effective mass). 

The expression does not take into account the mass profile of a galaxy. We wish to understand the effects of mass frequency relatively in terms of the radial distance from a center of mass relative to the mass profile of a galaxy. We accomplish this using the percent difference change of the modeled velocity to the effective velocity. The relation between the effective mass M_e and bound mass M_b is then the bound mass times the percent difference:

We then plot both the bound (purple) and effective (red) mass. The point where the effective mass rises above the bound is where the count of mass measures exceeds the count bound and, where classical behavior ceases and quantization begins … approximately 9.32848 10³ light-years. We call this the Quantization Crossover.

And when we integrate the mass density profile for the Milky Way into the expression, we produce the effective velocity (red). The blue curve represents Newton’s expression.

The expression is solved where v_e=v_m. Importantly, the input data must come from a physically significant source (i.e. mass, luminosity, etc.).

One might contend that using a velocity profile as the source data to get a velocity profile is a physically inappropriate means of describing the velocity of a star. We offer this expression as a compromise to a detailed mass profile (for which there is little data available).

While not ideal, the modeled velocity offers a physically correlated value representative of the mass profile as a function of the mass along the path of a star. Thus, in the classical sense of Newton's expression, the modeled velocity is a function of G, mass M and distance R, all represented by v_m.

Any solution where v_e≠v_m will cause a skew between the two curves such that the effective and modeled velocities separate. This is the case at the peak of the graph, due to discrepancies in the MOND mass models. In other words, that portion of the MOND modeling is physically incorrect.

Below, we present an example of what happens when values for v_m are not an accurate physical description of star velocity. The red and green curves diverge.