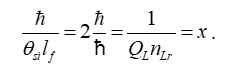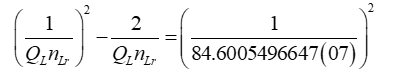—————————— read pre-print on research gate (new window) ——————————

• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.

• Q_Ln_Lr, also known as the Informativity differential describes the length contraction associated with discrete measure.
• Q_L is the fractional portion of a count of l_f when engaging in a more precise calculation.
• n_Lr describes the count of l_f representative of the position of an observable with respect to the frame of a center of mass.
• h is Planck’s constant.
• ħ is the reduced Planck constant, 1.054571817 10^-34 m² kg s^-1. When accounting for the Informativity differential at the upper count bound, this term is not italicized (i.e., ħ=1.0545349844(45) ^-34 m² kg s^-1).
• r_q is the quantization ratio (n_θθ_si)/RND(n_θθ_si). It describes the relation between the discrete and non-discrete frames of reference.
• RND(n) is a function; round to the nearest whole-unit value.

In addition to the well-known classical expressions for the reduced Planck constant, MQ offers an alternative. We approach the calculation anew, as a function of the Planck momentum θ_si which in turn is resolved as a measure of the fine structure constant. Several principles are needed to carry out the calculation.

The first regards frames of reference. There are three physically significant frames needed to instantiate the foundations of physics. They are, the:

• Reference Framework — This is the framework of the observer where properties of the reference (AB) are observed. With respect to the standard understanding, this framework differs only in that measure is a count function of discrete length measures equal to one.
• Internal Framework — This framework shares properties with the Reference Framework. It is characterized as some known count of the reference describing where count properties of the reference (BC) are observed.
• System Framework — This framework is characterized by the property of measure of non-discreteness, that being the framework of the universe that contains the phenomenon (AC).

Of these, there are also two significant domains of physical description. The first domain includes the description of phenomena with respect to other phenomena in the universe. The second domain includes the description of phenomena with respect to the universe.

We identify first domain descriptions as self-referencing; that is, descriptions where the notions of length, mass, and time are described by relativity.

Conversely, the universe can be treated as an expanding sphere of information. Such a system carries with it an emergent property, the three dimensional measures. They can be calculated knowning only the radial rate of expansion. With this, we can then recognize two physically significant frames associated with the universe. First, there is the Internal Frame. Second, we have the System Frame. The Internal Frame describes the fundamental measures local to the frame of the observer. In that the measures are a constant property of the Internal Frame, we can appropriately recognize them as references, discrete and countable. At the same time, we recognize that the System Frame of the universe has no external reference. Therein, the System Frame is non-discrete. And finally, considering the difference between these two frames allows us to resolve expressions and values for the physical constants.

In addition to these three frames the reader will also need to be familiar with quantization ratios. Quantization ratios present a mathematical approach that allows us to correlate descriptions of phenomenon with respect to the discrete and non-discrete frames. The expression for a quantization ratio is

The count term n, in this case, can take on any integer value. [Quantization ratios][2] provide a discrete mathematical approach to correlating the System and Internal Frames. For instance, with respect to a description of elementary charge, its discrete description can be resolved by setting the bound quantization ratio (a fractional relation) equal to the difference. Another way to describe this is b-d=b/d at the lower bound.

The length contraction associated with discrete measure must also be accounted for and where an electromagnetic field is used, then the count associated with that measure is found at the blackbody demarcation. Thus far, demarcations associated with blackbody demarcation, elementary charge and charge couplings are each at the same count distance, n_Lr=84.60055. The values differ in the seventh digit, but otherwise can be used interchangeably.

With these principles we can approach a calculation of the reduced Planck constant by resolving the demarcation associated with blackbody radiation Q_Ln_Lr, the Planck momentum θ_si and fundamental length l_f. Thus,

When compared to the 2018 CODATA we find the value for ħ matches to ten digits.

We bring to the reader's attention that the first solution is resolved with respect to the upper count bound. As such, we do not italicize the term. The latter is resolved with respect to the demarcation. We have resolved the demarcation as a function of the defined value, but do not use this value to then resolve the value for ħ at the demarcation. Rather, the last calculation is carried out with respect to the elementary charge demarcation, as a representative proxy for this phenomenon. Otherwise, we'd simply resolve in calculation the initial defined input for ħ.

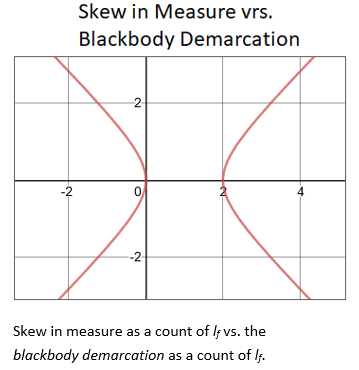
Finally, we consider a graphical presentation of ħ as a function of the Informativity differential. Setting x=ħ_f/θ_sil_f and y=1/n_Lr., we then have

The function can then be graphed to describe the magnitude of the Informativity differential^{(6,Sec. II.G)} associated with its measure. More importantly, we find that the vertex of the right parabola marks the count distance n_θ that corresponds to the blackbody demarcation^{(6,Apx. C)}.

The solution as displayed in the graph above for ħ/θ_sil_f falls on the point (2.000069857, 0.000139718) on the right parabola. The axis of symmetry for both parabolas lie parallel to the x-axis. The expression can also be reduced. With ħ_f=2θ_sil_f and ħ=θ_sil_f/Q_Ln_Lr, then

Substituting 1/Q_Ln_Lr for ħ/θ_sil_f, then

Written as such we find that the graph is a representation of a plane with both axis describing counts of l_f. Importantly, while the physical significance of the blackbody demarcation is understood, what is the physical significance of the vertex on the left parabola, with x and y coordinates that are each positive. Is this a physically important quality of the vacuum of space?

At present, we theorize that mass accretion in the universe is not entirely random, but instead a fixed rate function such that particles accrete near existing mass. This is to say that not all spacetime is equally conducive to the retention of new mass accreting into the universe. And as such, particles that do accrete into the universe are most likely to occur near existing mass. This can be investigated with respect JWST observations regarding proto-galaxy formation.