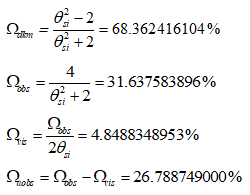—————————— read pre-print on research gate (new window) ——————————

• u₀, is the magnetic constant.

• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.
• Q_L is the fractional portion of a count of l_f when engaging in a more precise calculation.
• n_Lr describes the count of l_f representative of a change in position of an observable measured with respect to the observer’s frame of reference.
• Q_Ln_Lr, also known as the Informativity differential describes the length contraction associated with discrete measure.
• h is Planck’s constant.
• ħ is the reduced Planck constant, 1.054571817 10^-34 m² kg s^-1. When accounting for the Informativity differential at the upper count bound, this term is not italicized (i.e., ħ=1.0545349844(45) ^-34 m² kg s^-1).
• α_f^-1 is the fundamental form of the inverse fine structure constant defined with respect to the Target Frame.
• α_p^-1 is the Planck-like form of the inverse fine structure constant defined with respect to the Measurement Frame.
• α_c^-1 is the classical form of the inverse fine structure constant as adopted by the CODATA collaboration. This term accounts for length contraction associated with discrete measure.
• G is the gravitational constant, 6.6740779428(56) 10^-11m³kg^-1s^-2 such that its value considers the effects of length contraction associated with discrete measure at the upper count limit. Italicized G identifies a measure not at the limit (e.g., G=6.6738448362(53) 10^-11m³kg^-1s^-2 at the blackbody demarcation).
• Ω_vis is that domain of the universe that is presently visible.
• Ω_obs is that domain of the universe that is presently visible or will be visible given infinite elapsed time.
• Ω_dk is that domain of the universe that will never be visible.
• Ω_uobs is that domain of the universe that will eventually be visible but is not presently visible.

Measurement Quantization (MQ) is a physically significant approach that uses a nomenclature of counts of fundamental measures to express the classical laws of nature. In an analysis of Heisenberg’s Uncertainty Principle, the expression for the speed of light and for escape velocity we can resolve the minimum count values for each measure and the corresponding fundamental measures. Importantly, the fundamental measures are resolved with respect to the Internal Frame of an expanding universe which be shown occurs at a fixed radial rate equal in magnitude to half of the Planck momentum.

When taking a closer look at the fine structure constant and Planck’s expression for the ground state orbital of an atom, we can extend our understanding of the physical constants, uniting the electric and gravitational constant. This presents, for the first time, the ability to resolve a physically significant calculation of θ_si as a function of the fine structure constant (i.e. α_c=7.2973525693 10^-3), which in turn allows us to derive its value from a measure of the magnetic constant. With this, we can then proceed to resolve several more physical constants each equal to the physical significance of the fine structure constant, 11 digits.

Given the Informativity differential Q_Ln_Lr=0.49998253642 at the blackbody demarcation n_Lr=84.60055358 then,

The calculation can then be applied to resolve fundamental mass also to the same physical significance.

Although our calculations are a derivative of the CODATA definition of the fine structure constant, we can without conflict apply the derived value for θ_si to then resolve the Planck equivalent for the fine structure constant α*_p*⁻¹. We are afforded this by using a source measure for the fine structure constant that is not used in its assignment by the CODATA collaboration, therein avoiding conflict.

And with Planck’s expression for the ground state orbital of an electron and our newly resolved values for m_f and α_p as a function of θ_si, then

Given the defined value for the speed of light, this allows us to finally resolve the value for fundamental time.

Among other constants, we can also resolve the gravitational constant.

And we can resolve the reduced Planck constant now as a function of θ_si and l_f, both which now derive from the measure of the magnetic constant μ₀.

As we can see, there are many constants that can now be extended in precision. We will not address all possibilities, but we will note one final set. Those are the CMB power spectrum distributions, which are described by MQ such that

Notably, the MQ approach to resolving these distributions allows us to more easily resolve the spacetime relations between each of the distribution curves. And with our more precisely resolved value for θ_si, we find an even greater precision obtained.

These are among just a few opportunities where we can apply the expressions and new correlations obtained with an MQ approach to resolve more precise physically significant values for the physical constants. A more thorough analysis will certainly yield even more.