—————————— read pre-print on research gate (new window) ——————————

There are no inputs needed to resolve this expression.

• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• n_Tu is a count of t_f equal to the age of the universe.
• n_Mu is a count of m_f equal to the total of mass/energy in the universe.
• M_acr is the rate of mass accretion in the universe.
• M_vis is the mass in that domain of the universe that is presently visible.
• M_obs is the mass in that domain of the universe that is presently visible or will be visible given infinite elapsed time.
• M_dk is the mass in that domain of the universe that will never be visible.
• M_uobs is the mass in that domain of the universe that will eventually be visible but is not presently visible.
• M_tot is the mass in the entire domain that makes up the universe (i.e., 1 or 100%).
• M_f is the mass in that domain of the universe that is fundamental. Its physical significance describes a pivot point with respect to the remaining domains.
• V_U is the volume of the universe.
• A_U is the age of the universe.
• R_U is the radius of the universe.
• D_U is the diameter of the universe.

We can use the Measurement Quantization (MQ) approach to classical description to resolve the mass of the universe. The approach has advantage over prior methods in two ways. One, MQ describes a universe that accretes mass at a fixed rate. And two, MQ allows a calculation of the age of the universe as a function of CMB temperature.

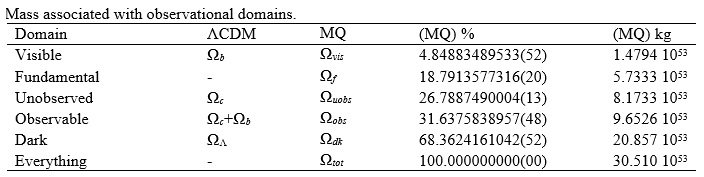
To resolve a more detailed understanding of mass, we will also need to understand observational domains. That is, with MQ we recognize that the universe can be divided into several domains and likewise the total mass is a composite of each of these domains. There are five.

The first, the fundamental domain Ω_f describes a mathematical pivot between the dark and observable domains. Those are defined such that the visible Ω_vis is that which we can presently measure. The observable Ω_obs is that which will be visible given infinite elapsed time. The unobserved Ω_uobs is that which is the difference between these two domains. And the dark Ω_dk is that which will never be observed due to the metric expansion of space. We identify the mass associated with each of these domains with the letter M.

Notably, all expressions for observational domains consist of only one physical constant θ_si. This is to say, observational domains do not change in magnitude relatively. Yet, the mass associated with the fundamental domain is a known function of the age of the universe A_U. This is increasing. With this, we recognize that the total mass of the universe must also be increasing.

With this, we then carry out calculations to resolve the rate of mass accretion.

And with this we need only the age of the universe to resolve the total. The individual domains are then a percentage of that total.

There are several principles at work in this derivation. For one, the derivation presumes that the relation of length, mass, and time are scalable to a description of cosmological phenomena. This is established, for instance in this article regarding the derivation of the observational domains. There are also notable conflicts where this is not found true (i.e., faster than light travel). Importantly, there exists no observation supporting faster than light travel.

Also important regards the coincidence of observational domains to those phenomena recognized as dark energy and dark matter. While there appears to be a significant physical correlation, observational domains are not meant to replace these placeholder terms. A full description of all the features associated with these phenomena can be found at the respective linked articles.

Lastly, MQ rests on physical support for the notion of measure as discrete references observed relative to the Internal Frame of the universe. MQ recognizes that there are no references external to the universe and as such the System Frame of the universe is non-discrete. The difference between these frames can be used to derive expressions and values for the physical constants and the laws of nature.

Importantly, MQ predicts a length contraction effect associated with discrete measure. The effect is not described by relativity. It can be measured with respect to existing CODATA publications of the physical constants.

In the introductory paper entitled, Measurement Quantization, each measure for G and ħ published in the 2010, 2014, and 2018 publications is calculated and shown to be a consequence of this effect, thus providing physical support for the MQ approach to classical description.