—————————— read pre-print on research gate (new window) ——————————

• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• A_U is the age of the universe.
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.

• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• D_U is the diameter of the universe.
• n_L, n_M and n_T are physically significant discrete counts of l_f, m_f and t_f respectively.
• n_Tu is a count of t_f equal to the age of the universe.
• n_Lu is a count of l_f equal to the diameter of the universe.

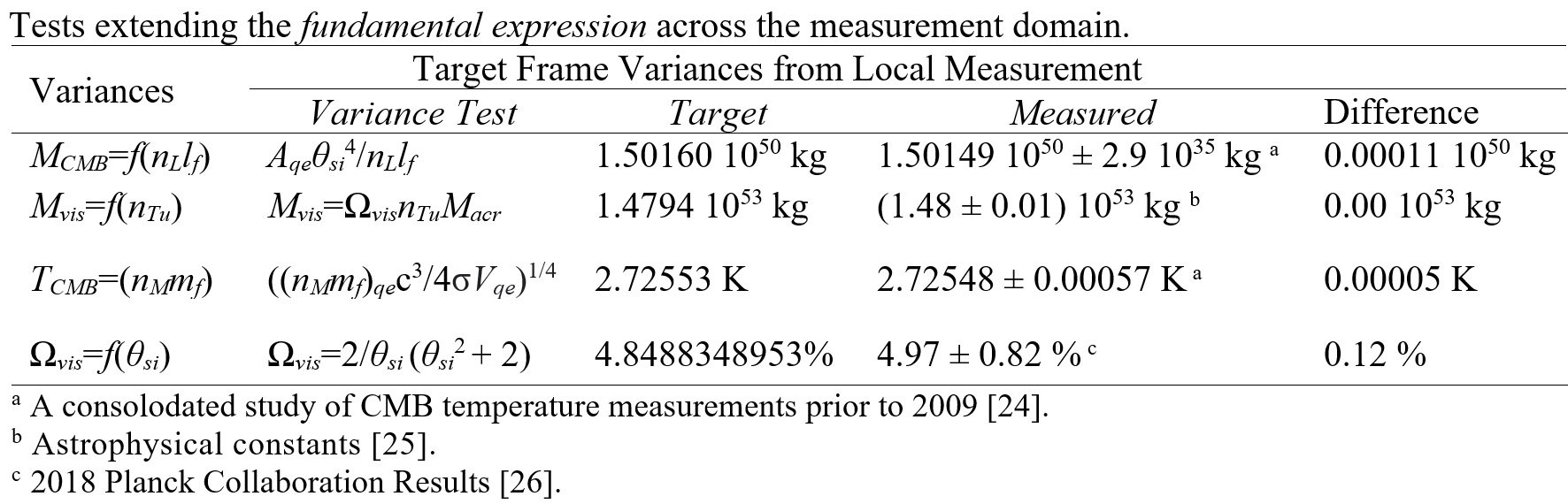
We calculate the age of the universe using the expression for the Planck momentum - also called the fundamental expression, l_fm_f=2θ_sit_f as a way to correlate length, mass and time between the Internal Frame and System Frames of the universe. This is achieved through scaling.

A scaling of the fundamental expression is physically supported in two ways. First by paradox; where we first establish a physical relationship, then an argument against scaling argues for a non-constant speed of light. This is not observed.

It follows, are attention then turns to establishing physical significance. With respect to the table presented above, we isolate functions each representing primarilly one term in the fundamental expression as a function of CMB formation in the earliest epoch. We compare those Measurement Quantization (MQ) calculations with measurements made today to assess the significance of the fundamental expression when scaled as a function of cosmological phenomena across epochs. And, as expected, we find digit-for-digit correspondence to the same precision afforded by measurement. Therein, to the precision offered by these results, we establish a physical correlation between scaling and measurements of cosmological observations.

By usual calculation, one determines the density of the CMB in the past or present by considering the rate of expansion and the age of the universe. Using MQ we reverse the calculation. Why? Because MQ provides a one parameter approach to a description of early universe events. Specifically, MQ can be used to show that the universe accretes mass at a steady rate.

MQ can also be used to describe a quantum epoch, a period when the universe is unable to expand at the speed of light, because points internal to the universe are unable to reference discrete points external to the universe. The rate of expansion is described by

This tells us that the quantum epoch lasts for 363,312 years. Accounting for time dilation between epochs, this appears as 678,894 years of mass accretion relative to an observer in the expansionary epoch. And knowing the total accreted mass - which then constitutes the CMB - and knowing the expressions for diameter and age of the universe and the resultant density, we can resolve the CMB temperature.

We then reverse the equations and solve for the age of the universe.

And finally, we use an expansion of the fundamental expression to resolve the diameter of the universe and the relation of fundamental mass to diameter and age.

The latter expression defines fundamental mass, an unchanging property of the relation describing length and time in a system.  As discussed in the article on frames of reference, this expression exemplifies the correlation between a description of mass which is also a description of the universe such that m_f is understood externally and D_U and A_U are understood internally.