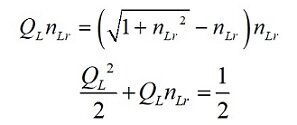—————————— read pre-print on research gate (new window) ——————————

There are no inputs when deriving the Informativity differential.

• Δθ corresponds to gamma γ, representing the measurement difference from that value predicted with general relativity in the angle of deflection of light passing through a gravitational field.
• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• r is the distance between an observer and a target.
• M is the mass of a phenomenon.
• Q_L is the fractional portion of a count of l_f when engaging in a more precise calculation.
• n_Lr describes the count of l_f representative of the position of an observable with respect to the frame of a center of mass.
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.
• G is the gravitational constant, 6.6740779428(56) 10^-11m³kg^-1s^-2 such that its value considers the effects of length contraction associated with discrete measure at the upper count limit. Italicized G identifies a measure not at the limit (e.g., G=6.6738448362(53) 10^-11m³kg^-1s^-2 at the blackbody demarcation).

Special and General Relativity implement a geometry between an observer and an observed phenomenon such that the measures of length, mass and time are shown to be a distorted function of an inertial and/or gravitational mass. Using a Measurement Quantization (MQ) approach to the description of phenomena, a new effect is resolved that describes the contraction of length (only). This effect is not related to relativity. Rather, it is a property of discrete measure, a function of the discrete Internal Frame of the universe. We call this effect, the Informativity differential, specifically because it describes the fractional count Q_L of a more precise calculation of fundamental reference measure. Importantly, as this effect is a geometric function applicable only where there are two or more dimensions, it is applicable only with respect to length.

The Informativity differential can be described as the remainder count of a more precise calculation of discrete length measures. Because Q_L is less than the reference count Q_L < n_Lr >= 1 of l_f, Q_L has no physical significance at each increment of elapsed time t_f. Moreover, the loss of Q_L describes gravitational curvature with quantum precision.

While GR interprets space as curved, this is not the case for MQ. In that the fundamental measures are physically significant references, it follows that phenomena - which reside non-discretely with respect to non-discrete System Frame of the universe - cannot be observed with greater precision than a whole unit count of the Internal Frame references. Thus, MQ does not describe a curved spacetime. Rather, it describes a count differential, lost with each increment count in elapsed time. Curvature is then an emergent feature of this loss of length.

The Informativity differential can be physically assessed with respect to the reduced Planck, and gravitational constants. In that this effect increases with decreasing distance, we consider two types of measurements, that most associated with blackbody radiation - also known as the blackbody demarcation (i.e., we denote measures resolved at this distance with italics) - and that associated with the upper count bound. The latter coincides with macroscopic measurements (i.e., a time-of-swing measure of G). We identify measurements resolved macroscopically without italics.

In the table presented in Experimental Support, the latter four lines describe the results of calculations at these two specific counts. Importantly, all values published by the CODATA collaboration except for the value of G in 2018 are described correctly digit-for-digit. The 2018 result is the result of a mis-application of Planck's expressions and is calculated and described in the associated pre-print.

As many measurements are macroscopic and such that the length contraction described by the Informativity differential macroscopically is less than the physical significance of existing measurement technology, using the upper count bound result Q_Ln_Lr=1/2 is appropriate. We present that result here,

To resolve the length contraction associated with an electromagnetic phenomenon, we set all component measures respective of a shared count distance at the electromgantic demarcation. We can likewise resolve G at the blackbody demarcation. For simplicity, we most often resolve expressions at the upper count bound. Recall also, we represent upper bound terms without italics, for instance,

A comparison of these calculations is presented in the table below.

Finally, if we look to Newton’s expression for gravitational curvature, we can describe the magnitude of the Informativity differential at different distances, first as a function of G/r² and then as a function of ħ.