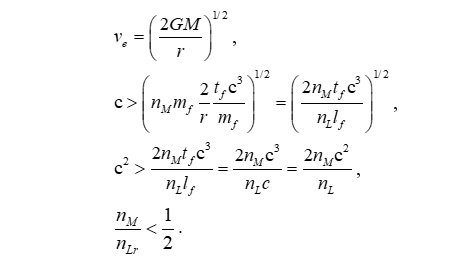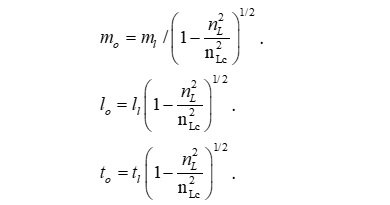—————————— read pre-print on research gate (new window) ——————————

There are no inputs needed to resolve these expressions.

• n_L, n_M and n_T are physically significant discrete counts of l_f, m_f and t_f respectively.
• n_Lr describes the count of l_f representative of a change in position of an observable measured with respect to the observer’s frame of reference.
• n_Lo is the count of l_f observed with respect to the observer’s frame of reference.
• n_Ll is the count of l_f measured with respect to the observer’s frame of reference.

Singularities in modern theory are encountered in situations such as General Relativity (GR) when describing the center of a black hole. Some approaches describing the earliest epoch of our universe also encounter singularities, a state where expressions resolve values infinite or undefined. We identify this property of physical description as a singularity. Singularities have been an issue with respect to physical description for more than a century.

Herein, we offer a new approach to classical description that does not produce singularities. We call this approach Measurement Quantization (MQ). With respect to the MQ approach, the notions of length, mass, and time are described using counts n_L, n_M, and/or n_T of fundamental units of measure l_f, m_f, and/or t_f. Different from, for example, Planck Units, MQ establishes the physical significance of the fundamental measures by means of a discrete description of gravitational curvature.

Importantly, MQ predicts a new form of length contraction - associated with discrete measure - which can be confirmed with respect to existing CODATA publications. Using MQ, we can then resolve expressions and values for the physical constants and the laws of nature. We provide links to relevant discussions herein, but for the purposes of this discussion our focus regards singularities and why MQ descriptions of phenomena are not subject to this mathematical conundrum.

Why? Specifically because - in conjunction with a discrete description of gravitational curvature - and an analysis of the expressions for Heisenberg's uncertainty principle (specifically at the Planck scale bound), escape velocity and the speed of light, we resolve that measure relative to frames within the Internal Frame of the universe is discrete and countable. And such that there are no external references to the universe, we recognize that the System Frame of the universe is non-discrete.

Therein, when using the MQ nomenclature we often find such descriptions - specifically descriptions that describe a geometry - reduce such that all measures cancel out, leaving only the counts. And, such that all counts must reflect a whole-unit value between one and the Planck frequency, we find that no expression can have a result that is undefined. We proceed with the expression for escape velocity at the bound as one way in which to demonstrate this quality.

To clarify, when writting expressions using an MQ nomenclature we distinguish counts of l_f using two terms. The term n_Lr describes the count of l_f between a phenomenon or an observer and the center of a gravitational mass. The count n_L describes the count of l_f representative of a change in position. The terms can be used interchangably, but are meant to provide additional context to an expression, especially expressions such as Heisenberg's uncertainty principle, where both terms can exist at the same time.

In all cases, we find that the count value for n_Lr must be one or greater. Thus, we cannot find a ratio undefined. The expression also tells us that n_Lr must be greater than two times n_M.

Consider now MQ descriptions describing the distortion of measure with respect to motion, the same phenomenon also described by Special Relativity (SR).

As noted, there are physically significant upper and lower count bounds with respect to each dimension. Many phenomena we observe in nature (i.e. dark matter) are a consequence of measurement bounds, at either end of the measurement domain.

We bring also to your attention that the speed parameter (n_L/n_Lc)² is physically equivalent to its gravitational counterpart (n_M/n_Lr). This is demonstrated in the article discussing the Equivalence Principle. The equivalence principle allows us to extend the observations made above regarding motion to also include gravitation. But unlike the traditional approach to equivalence, MQ does not present as an axiom equivalence.

You can use MQ to derive the equivalence principle. MQ has the unique advantage of each term having a physically significant correlation to measure. And such that all terms are physically significant, and such that classical expressions can be reduced to MQ form, we no longer need to consider field theory as an approach to correlating the phenomenon of gravitation with motion. Both phenomena can be written in terms of counts of the fundamental measures, physically assessed and correlated to demonstrate that the distortion of measure with respect to motion is a geometric equivalence with that of gravitational curvature. And most important, such that all counts must be in the range of one to the Planck frequency, no description regarding motion or gravitation can be undefined.