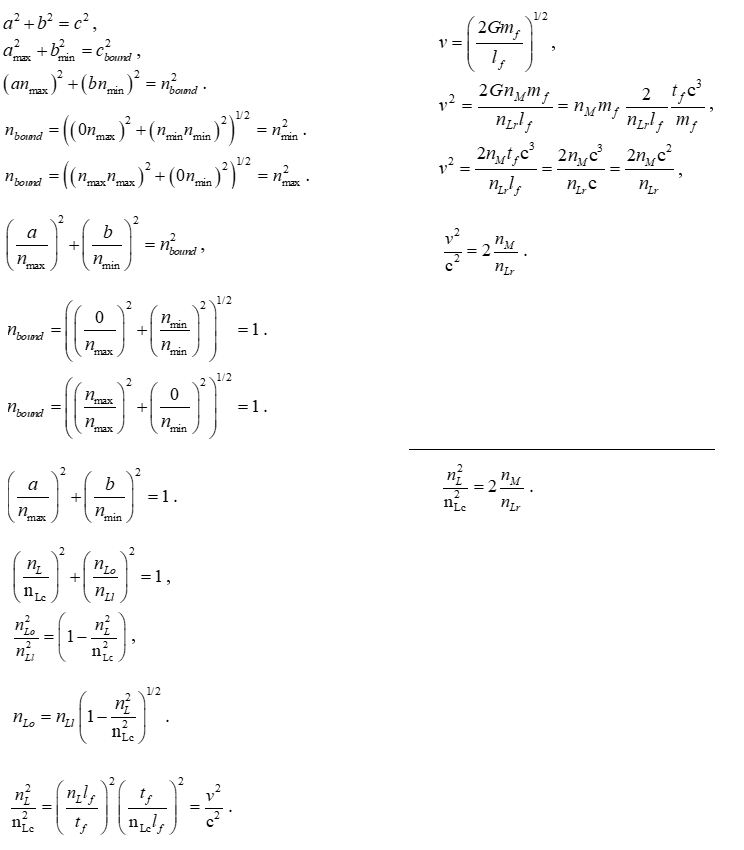—————————— read pre-print on research gate (new window) ——————————

• Initially we recognize that the gravitational constant may also be written as (l_f/t_f)³ t_f/m_f. We also recognize that relation described by the Pythagorean theorem.

• l_f, m_f and t_f are the fundamental measures, more precise expressions for Planck’s units – length, mass, and time – that consider the effects of length contraction associated with discrete measure.
• θ_si can be measured as the polarization angle of quantum entangled X-rays at the degenerate frequency of a maximal Bell state. As an angle θ_si=3.26239 rad ± 2 μrad; as a momentum θ_si=3.26239030392(48) kg m s^-1 and with respect to the Target Frame, θ_si has no units. The relation of angle and mass is mathematically demonstrated, as well, by No-Ping Chen, et. al.
• n_Lc describes the count of l_f* representative of a change in position of light measured with respect to the observer’s frame of reference.
• n_Lo is the count of l_f observed with respect to the observer’s frame of reference.
• n_Ll is the count of l_f measured with respect to the observer’s frame of reference.
• n_L, n_M and n_T are physically significant discrete counts of l_f, m_f and t_f respectively.
• Q_L is the fractional portion of a count of l_f when engaging in a more precise calculation.
• l_l is a measure of length with respect to the observer’s measurement frame.
• l_o is the observed length subject to the effects of motion and/or gravitation.
• m_l is a measure of mass with respect to the observer’s frame of reference.
• m_o is the observed mass subject to the effects of motion and/or gravitation.
• t_l is a measure of time in the local frame of reference.
• t_o is the observed time subject the effects of motion and/or gravitation.
• v is velocity measured between an observer and a target.
• c is the speed of light which may also be written as c=n_Ll_f/n_Tt_f=299,792,458 m/s such that n_L=n_T=1 is physically significant.

With respect to the principle of equivalence, modern theory does not offer a classical description of motion and gravitation that can be used to derive equivalence from first principles. The reason for this stems from mathmatically incompaitble descriptions of these phenomena. Einstein correlates these two frames using the principle of equivalence.

When using the Measurement Quantization (MQ) approach to classical expression, the distortion of measure relative to inertial and gravitational frames is resolved as a geometric feature of an expanding sphere of information. MQ does not require a principle of equivalence. Importantly, the effects described by SR and GR are resolved with MQ using a single physical instantiation without field theory or calculus (the latter obscures the discrete features of referential systems of measure).

MQ describes both gravitational and inertial frames as a geometric property of the System and Internal Frames of the universe. MQ expands the existing classical nomenclature, separating the scalar counts n_L, n_M, and n_T from the reference measures l_f, m_f, and t_f. In this way, we establish physical correlation while also preserving and separating the geometric properties of a physical description.

Starting with the MQ form of Einstein's expression for SR, let us reorganize the terms and expose Beta.

Thus, we resolve a description of two frames having relative motion. We now turn our attention to a description of the [gravitational frame][1] using the same approach. Beginning with the expression for escape velocity, we write all terms as a function of the fundamental measures while exposing Beta to one side of the equation.

Setting the two expressions equal to one another, then

Thus, we have resolved a discrete description of equivalence not as a hypothesis, but as an outcome. The two phenomena are one and the same.

Notably, there are no measure terms - l_f, m_f and t_f - in the final expression. All measures have cancelled leaving only the count terms. The same happens when conducting an analysis of Heisenberg's uncertainty principle with respect to the Planck scale bound. Both results bring to the reader's attention that the fundamental measures play no role with respect to these geometries.

We also bring to the reader's attention that the reduction of G to its corresponding fundamental measures must be carried out with the MQ discrete solution to G, not the classical solution which rests on use of the Planck Mass expression. The Planck Mass cannot be physically assessed. The inability to physically assess the relation is why solutions using escape velocity have never been considered an acceptable solution to discribing the distortion of measure with respect to a gravitational frame.